

Alessandro Rosa
Freelance programmer
c/o Locatelli,
Via Cappuccini 116/A,
I-72100 Brindisi, Italy
We show the equivalence between Borel's regular sets model and the Liouville formula for the approximation of irrationals through rational numbers. The Diophantine-Liouville dichotomy can be resolved via sequences of transfinitely many approximants.
The existence of non-linearizable hedgehogs is purely theoretical and their electronic visualization is not feasible.
We show that the non-linearizable hedgehog for polynomials
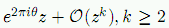
is a locally connected, plane-filling Julia set with Hausdorff dimension 2, spreading radially everywhere inside a bounded non-empty region.