Differential Equations and Control Processes
(Differencialnie Uravnenia i Protsesy Upravlenia)

The Cyclicity Problem for Two-dimensional Polynomial Systems

Author(s):

V. G. Romanovski

Center for Applied Mathematics
and Theoretical Physics, University of Maribor},
CAMTP, Krekova, 2,
Maribor, SI-2000,
Slovenia.

valery.romanovsky@uni-mb.si

A. S. Jarrah

New Mexico State University,
Department of Mathematical Sciences,
New Mexico State University,
Las Cruces, NM 88003,
USA

ajarrah@nmsu.edu

R. Laubenbacher

Virginia Bioinformatics Institute,
1880 Pratt Drive Blacksburg,
VA 24061, USA

reinhard@almaren.bioinformatics.vt.edu

Abstract:

The problem of small limit cycles bifurcations (the cyclicity problem) is considered for the system with homogeneous cubic nonlinearities

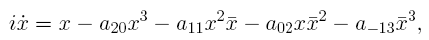
and for the cubic system

where akj are complex parameters and x=u+iv. Considering as an example the first system we show that using algorithms of computational commutative algebra one can easily solve the cyclicity problem in the case when the ideal of focus quantities is a radical ideal.

In the case of the second system it appears the ideal of focus quantities is not a radical one. Nevertheless using the monoid structure of the focus quantities we are able to find a basis of the ideal and to solve the cyclicity problem for "almost all" values of parameters of the system.

Full text (pdf)