Дифференциальные Уравнения
и
Процессы Управления

Проблема цикличности для двумерных полиномиальных систем

Автор(ы):

В. Г. Романовский

Center for Applied Mathematics
and Theoretical Physics, University of Maribor,
CAMTP, Krekova, 2,
Maribor, SI-2000,
Slovenia.

valery.romanovsky@uni-mb.si

A. S. Jarrah

New Mexico State University,
Department of Mathematical Sciences,
New Mexico State University,
Las Cruces, NM 88003,
USA

ajarrah@nmsu.edu

R. Laubenbacher

Virginia Bioinformatics Institute,
1880 Pratt Drive Blacksburg,
VA 24061, USA

reinhard@almaren.bioinformatics.vt.edu

Аннотация:

Рассмотрена проблема бифуркаций малоамплитудных предельных циклов (цикличности) для системы с однородными кубическими нелинейностями

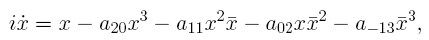
и кубической системы

где akj -- комплексные параметры, x=u+iv. На примере первой из систем показано, что с использованием алгоритмов вычислительной коммутативной алгебры проблему цикличности можно легко решить в тех случаях, когда идеал фокусных величин является радикальным идеалом. В случае второй системы идеал фокусных величин, по-видимому, не является радикальным. Тем не менее, на основе использования моноидальной структуры фокусных величин найден базис идеала фокусных величин и решена проблема цикличности для "почти всех" систем такого вида.

Полный текст (pdf)